트리는 나무의 형태를 뒤집은 것과 같은 형태의 자료 구조이다.
이진 트리(Binary Tree)는 최대 2개의 자식을 가질 수 있는 트리이다.

길이(length)란 출발 노드에서 목적지 노드까지 거쳐야 하는 가지의 수를 의미한다. 여기서 주의해야 할 점은 출발 노드가 루트 노드가 아닐 수 있고, 목적지 노드도 리프 노드가 아닐 수 있다는 점이다.

깊이(Depth)란 루트 노드에서 특정 노드까지의 길이를 의미한다.

높이(Height)란 루트 노드에서 가장 깊은 노드까지의 길이를 의미한다.

포화 이진 트리(Full binary tree)는 리프 노드를 제외한 모든 노드가 2개의 자식을 가지고 있는 트리이다. (원래도 리프 노드는 자식을 가지지 않음)
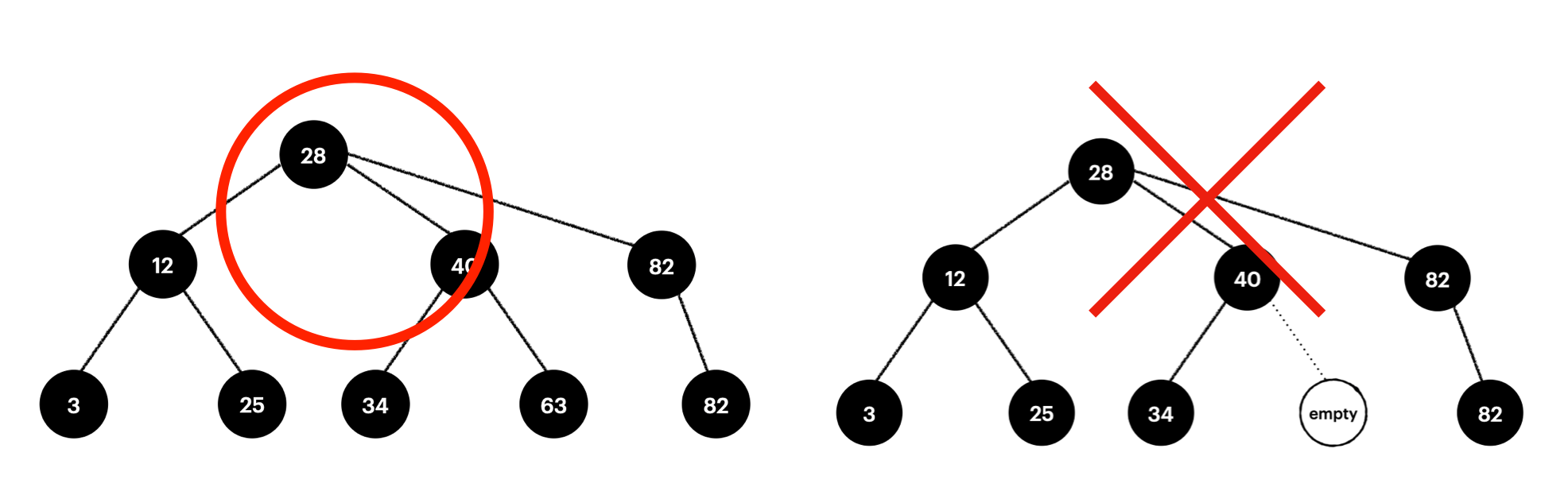
완전 이진 트리(Complete binary tree)는 모든 노드를 왼쪽 자식부터 차근차근 채워진 트리이다.

높이 균형 트리(Height balanced tree)는 왼쪽 자식 트리와 오른쪽 자식 트리의 높이가 1 이상 차이 나지 않는 트리이다.

이진 트리는 많은 양의 노드르르 낮은 높이에서 관리할 수 있다는 점에서 데이터 활용의 효율성이 높다. 데이터 저장, 탐색 등의 다양한 목적에서 이 자료 구조를 사용할 수 있다. 앞으로는 편향된 이진 트리의 경우, 한 쪽으로 몰린 바르지 못한 자료 구조로, 높이 균형을 맞추는 방법도 배우게 될 것이다.
이진 트리의 구현 과정에서는 포인터를 이용하면 효과적으로 데이터를 관리할 수 있다. 다음과 같은 구조체를 사용할 수 있다.
typedef struct Node{
//포인터가 두 개나 사용되기 때문에 정수형 데이터 하나만 저장하기엔 아까운 자료 구조이긴 하지만,
//오늘은 구현 방법을 익히는 것이니 쉽게 넘어가자.
int data;
struct Node *leftChild;
struct Node *rightChild;
}이진 트리에 담긴 데이터를 하나씩 방문해 출력하는 방법으로는 대표적으로 3가지 방법이 있다.
1) 이진 트리의 전위 순회 (preorder)
자기 자신을 출력 -> 왼쪽 자식 방문 -> 오른쪽 자식 방문
2) 중위 순회 (inorder)
왼쪽 자식 방문 -> 자기 자신 출력 -> 오른쪽 자식 방문
가장 왼쪽의 노드부터 출력해서 오른쪽으로 간다.
3) 후위 순회 (postorder)
왼쪽 자식 방문 -> 오른쪽 자식 방문 -> 자기 자신 출력
루트 노드가 가장 마지막에 출력된다는 특징이 있다.
이 세 가지 방법을 구현한 코드는 여기에서 확인할 수 있다.
'[알고리즘] 문제 풀이 > 자료구조 | 알고리즘' 카테고리의 다른 글
| 2021.2.27 TIL : [자료구조] 그래프의 개념과 구현 (0) | 2021.02.27 |
|---|---|
| 2021.2.25 TIL : [자료구조] 순차 탐색과 이진 탐색(Sequential Search and Binary Search) (0) | 2021.02.26 |
| 2021.2.21 TIL : [자료구조] 계수정렬(Counting Sort) (0) | 2021.02.24 |
| 2021.2.21 TIL : [자료구조] 퀵 정렬(Quick Sort) (0) | 2021.02.21 |
| 2021.2.20 TIL : [자료구조] 선택 정렬과 삽입정렬 (0) | 2021.02.20 |




댓글