여러 문제들을 분류해 보면 주어진 문제의 해를 구하는 알고리즘이 전혀 존재하지 않는 풀 수 없는 문제들이 존재한다. 그리고 풀 수 있는 문제들이 존재한다. 풀 수 있는 존재들을 분류 하면 현실적인 시간 내에 풀 수 없는 문제들과 현실적인 시간 내에, 즉 합리적인 시간 내에 풀 수 있는 문제들이 있다. 오늘 배운 NP-완전 문제들은 현실적인 시간 내에 풀 수 없는 문제들에 속할 것이라고 추정되는 문제들이다.
현실적인 시간은 다항식 시간(polynomial time)을 의미한다. 입력의 크기를 n이라고 할 때 n의 다항식으로 표시되는 시간을 말한다. 즉, O(n^k) 나 O(3nk + 5nk -1), O(n log n) 등이다. 비다항식 시간의 예로는 O(2^n) 혹은 O(n!) 등이 존재한다.
문제에서 요구하는 바에 따라 또 여러 가지로 분류가 가능하다. 첫 번째는 Yes/No 문제이다. 그래프 G에서 해밀토니안 경로(사이클)가 존재하는가? 하는 문제가 그 예라고 할 수 있다. 여기서 해밀토니안 경로(사이클)은 모든 정점을 한번만 지나는 경로(사이클)를 말한다. = 해밀턴 경로(사이클)
최적화한 결과를 요구하는 문제도 존재한다. 에지에 가중치가 있는 그래프 G에서 길이가 가장 짧은 해밀토니안 경로(사이클)의 길이를 구하는 문제가 대표적인 최적화 문제이다. 이 문제는 Traveling Salesman Problem (외판원 문제)로 장사꾼이 살고 있는 도시에서 모든 도시로 1회씩 방문하여 판매하고 집에 돌아오는 최소 비용을 구하는 것으로 잘 알려져 있다.
NP-Complete(NP-완전) 의 이론
이 문제는 Yes/No의 대답을 요구하는 문제(=Decision 문제)에 국한된다. 그렇지만 이 문제는 최적화 문제와 밀접한 관계를 갖고 있다. 이 이론은 문제를 현실적인 시간(다항식 시간) 안에 풀 수 있는가에 관한 이론이며, 거대한 군을 이루고 있다. 이 군 중에 한 문제라도 현실적인 시간에 풀면 다른 모든 것도 저절로 풀리는 논리적 연결관계를 갖고 있다.
현재까지의 연구 결과에 따르면 어떤 문제가 NP-Complete임이 확인되면 지금까지의 연구 결과로는 이 문제를 현실적인 시간에 풀 수 있는 방법은 없다. 하지만 현실적인 시간에 풀 수 없음을 증명하지는 못했다. P=NP 문제는 현재 21세기 7대 백만불짜리 문제 중의 하나이다. 만약 문제 A와 B가 있고, 문제 B가 현실적인 시간 안에 풀 수 있는 쉬운 문제이며 문제 A가 문제 B로 현실적인 시간 안에 쉽게 변형 된다면 문제 A도 쉽다고 말할 수 있다. (즉, Yes/No 문제라고 할 때, 문제 A의 답이 Yes(No)일 때 문제 B의 답도 Yes(No)가 되는 경우 변형 가능한 것으로 판단)
다항식 시간 변환
문제 A의 사례 a를 문제 B의 사례 b로 바꾸되 아래 성질을 만족하면 다항식 시간 변환이라 하고 이를 a <= b로 표기한다.
1) 변환은 다항식 시간에 이루어진다.
2) 두 사례의 답은 일치한다.
문제 A를 푸는 알고리즘
1) 문제 A를 다항식 시간에 문제 B로 변환한다.
2) 변환된 문제 B를 푼다
3) 문제 B의 대답이 Yes 이면 Yes, No이면 No를 리턴한다.
P와 NP
P는 polynomial 을 의미한다. 다항식 시간 안에 Yes 또는 No 대답을 할 수 있으면 P이다.
NP는 Nondeterministic Polynomial로, Non-Polynomial의 준말이 아니다! Yes 대답이 나오는 해를 제공했을 때, 이것이 Yes 대답을 내는 해라는 사실을 다항식 시간에 확인해줄 수 있으면 NP이다.
어떤 문제가 NP임을 보이는 것은 대부분 아주 쉽다. NP-Complete 증명에서 형식적으로 확인하고 넘어가는 정도이다. 대표적인 NP문제로는 해밍턴 사이클 존재 여부를 판단하는 문제가 있다. 다음 예를 보면 이해하기 쉽다.

NP-Complete(NP-완전)/Hard(NP-난해)
다음 성질을 만족하면 문제 L은 NP-Hard이다.
1) 모든 NP 문제가 L로 다항식 시간에 변환가능하다. (NP문제를 L문제로 바꿔서 해결할 수 있다면 이 때 L문제를 NP-Hard라고 한다.)
다음 두 성질을 만족하면 문제 L은 NP-Complete이다.
1) L은 NP이다.
2) L은 NP-Hard이다.
※NP-Complete는 NP-Hard의 일부이므로 NP-Complete인 문제를 NP-Hard라고 불러도 맞다.
※NP-Complete의 성질 1은 대부분 자명하므로 핵심에 집중하기 위해 NP-Hard애 초점을 맞추자.
NP-Hard 증명의 예
해밀토니안 사이클 문제가 NP-Hard임은 알고 있다 가정하자.
이를 이용해서 외판원 문제(TSP)가 NP-Hard임을 보일 수 있다.
해밀턴 사이클로 TSP가 가능하려면 TSP 문제에 주어지는 그래프 에지의 가중치가 모두 1이라고 생각하면 된다. 해밀턴 사이클 문제의 instance A를 아래와 같이 TSP 문제의 instance B로 다항식 시간에 변화를 시킨다.
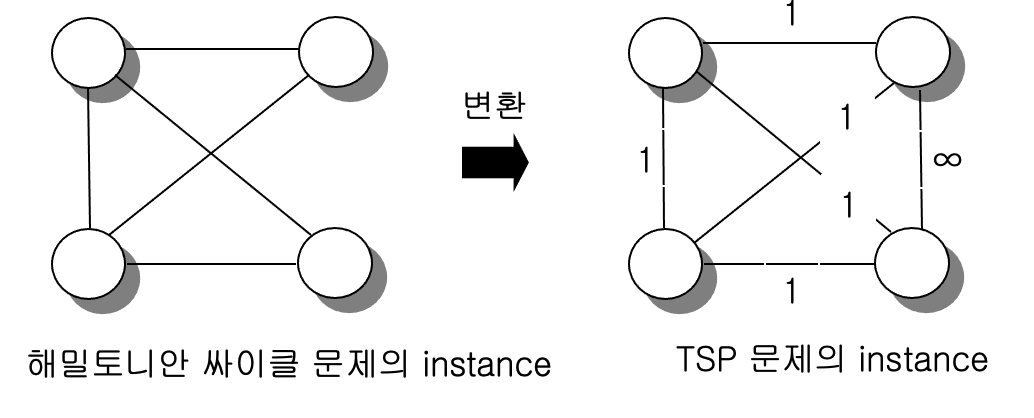
instance A가 해밀턴 사이클을 갖는다면 instance B는 길이가 4 이하인 해밀턴 사이클을 갖는다. (그래프의 vertex 개수가 n이면 4대신 n)
∴ TSP는 NP-Hard이다.
직관과 배치되는 NP-Complete 문제의 예
최단 경로 문제
- 그래프 G의 정점 s에서 t로 가는 shortest path는 다익스트라 알고리즘을 이용하여 간단히 구할 수 있다.
- 이 문제는 P에 속한다.
최장 경로 문제
- 반면, 그래프 G의 정점 s에서 t로 가는 longest path는 간단히 구할 수 없다.
- 이 문제는 NP-Complete에 속한다.
얼핏 보면 두 문제가 비슷한 문제처럼 보이지만, 두 문제의 난이도는 지금까지의 연구 결과로 봤을 때는 천지차이다.
최장 경로 문제
- 주어진 그래프에서 vertex s에서 t로 가는 길이 k 이상인 simple path가 존재하는가? 로 문제를 바꿀 수 있다. 바뀐 문제는 Decision문제가 된다.
- 두 점 사이의 해밀턴 경로 문제 : 주어진 그래프에서 정점 s에서 t에 이르는 해밀턴 경로가 존재하는가하는 문제이다. 이 문제는 NP-Complete로 알려져 있다.
▶ 두 점 사이 해밀턴 경로 문제의 instance A로부터 최장 경로 문제의 instance B로 다항식 시간 안에 변환이 가능하다.
instance A가 두 점 s와 t 사이에 해밀턴 경로를 갖는다 ↔ instance B가 두 점 s와 t 사이에 길이 4 이상인 (사실은 정확히 4인) 단순 경로를 갖는다. (그래프의 크기가 n이면 4 대신 n-1)
∴ 최장 경로 문제는 NP-Hard이다.
더 나아가면 해밀턴 경로 문제는 NP-완전 문제이고, 최장 경로 문제도 주어진 해가 가중치 있는 그래프 G에서 최장 길이인지 판단하는 데 걸리는 시간이 다항식 시간 내인 NP라는 점에서 최장 경로 문제도 NP-완전 문제라고 할 수 있다.
NP 이론의 유용성
왜 어떤 문제가 NP인지 구분하려고 할까?
어떤 문제가 NP-Complete / Hard 임이 확인되면 해당 문제에 대해 쉬운 알고리즘을 찾으려는 헛된 노력은 일단 중지한다. (존재하지 않기 때문에) 또한 주어진 시간 예산 내에서 최대한 좋은 해를 찾는 알고리즘 개발에 집중한다.(이 때, 찾는 해는 최적해가 아닐 수도 있다)
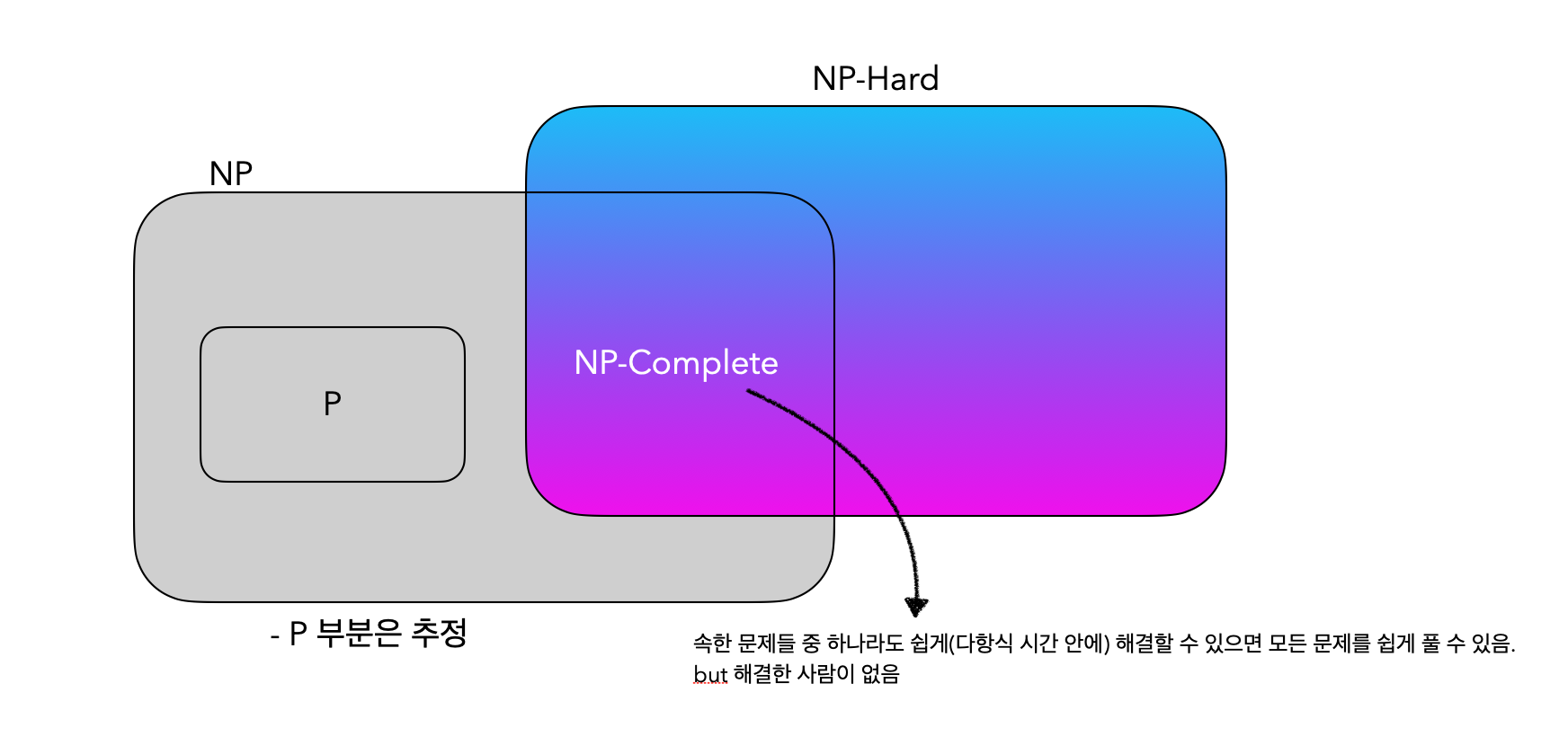
지금까지 밝혀진 NP와 NP-Complete / NP-Hard의 관계
'[알고리즘] 문제 풀이 > 자료구조 | 알고리즘' 카테고리의 다른 글
| [알고리즘] HashMap, TreeMap, HashSet, TreeSet (0) | 2022.02.12 |
|---|---|
| 2021.6.13 TIL : [알고리즘] 백트래킹 (BackTracking) (0) | 2021.06.13 |
| 2021.3.7 TIL : [알고리즘] 깊이 우선 탐색(Depth First Search) (0) | 2021.03.07 |
| 2021.2.27 TIL : [자료구조] 그래프의 개념과 구현 (0) | 2021.02.27 |
| 2021.2.25 TIL : [자료구조] 순차 탐색과 이진 탐색(Sequential Search and Binary Search) (0) | 2021.02.26 |



댓글